PID is a three-letter acronym that stands for Proportional–Integral–Derivative controllers. PID controllers or three-term controllers are control loop feedback (mechanism) controllers widely used in industrial control systems and various applications requiring continuously modulated control.

HISTORY

The PID controller is the most common form of feedback control. In 1911, the businessman and inventor Elmer Sperry created the PID control which combines these three actions. PID controllers were first used in the 1930s to control manufacturing processes. PID controllers were first used in the control of steam engines. The PID controller has been used in a variety of industries since its inception. PID controllers were first used in the 1950s in the control of nuclear power plants.

Each of those three words represents one of the three main components of a PID controller. PID controllers are used in all sorts of machines that need to be controlled, such as robots and cars. The most common use of PID controllers is in industry, where they are used to control factory machines. A PID controller takes a measured value, such as temperature or pressure, and adjusts an output, such as heating or cooling, to maintain the measured value at the desired setpoint.

The controller attempts to minimize the error by adjusting the process control inputs. PID controllers are commonly used to control temperature, pressure, flow, level, and speed loops.

The Three Responses of PID

Proportional Response

The proportional component depends only on the difference between the set point and the process variable. This difference is referred to as the Error term. The proportional gain (Kc) determines the ratio of output response to the error signal. For instance, if the error term has a magnitude of 10, a proportional gain of 5 would produce a proportional response of 50. In general, increasing the proportional gain will increase the speed of the control system response. However, if the proportional gain is too large, the process variable will begin to oscillate. If Kc is increased further, the oscillations will become larger and the system will become unstable and may even oscillate out of control.

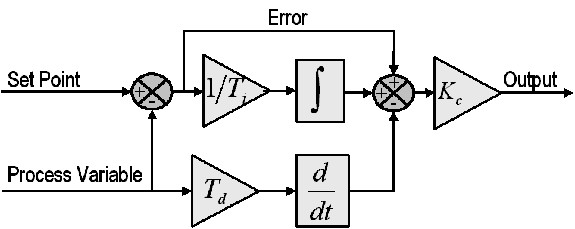
Integral Response

The integral component sums the error term over time. The result is that even a small error term will cause the integral component to increase slowly. The integral response will continually increase over time unless the error is zero, so the effect is to drive the Steady-State error to zero. Steady-State error is the final difference between the process variable and the set point. An integral windup occurs when integral action saturates a controller without the controller driving the error signal toward zero.

Derivative Response

The derivative component causes the output to decrease if the process variable is increasing rapidly. The derivative response is proportional to the rate of change of the process variable. Increasing the derivative time (Td) parameter will cause the control system to react more strongly to changes in the error term and will increase the speed of the overall control system response. Most practical control systems use very small derivative time (Td) because the Derivative Response is highly sensitive to noise in the process variable signal. If the sensor feedback signal is noisy or if the control loop rate is too slow, the derivative response can make the control system unstable

WORKING

The P Controller stabilizes the gain but produces a constant steady-state error.
The I Controller reduces or eliminates the steady-state error.
The D Controller reduces the rate of change of error.

ADVANTAGES

PID only acts on the error between the desired signal and the controlled signal. Hence, no extra measurements of the internal states are needed.
Easy to implement in hardware (through filters) and also easy to implement through microcontrollers, PLC, etc. No fancy codes to design… can be written by a middle-level programmer.

DISADVANTAGE

The controller is not really suited for nonlinear plants in general or in layman's language, and the controller may not assure the desired performance for a changing environment/ operating point. 

In high-end applications like fighter aircraft, submarines, precision robotics, economic models (stock market predictions), etc, mere fulfillment of the stable performance around a fixed operating region. 

The controller should be able to track a reference signal under various conditions (even though some of them may not be known).

Overall, the controller works well for most industrial/process applications but on the contrary no really suited for advanced applications for defense, robotics, financial models, etc.

REFERENCE 

REFERENCE 01